Cohomotopy group

In mathematics, particularly algebraic topology, cohomotopy sets are particular contravariant functors from the category of pointed topological spaces and point-preserving continuous maps to the category of sets and functions. They are dual to the homotopy groups, but less studied.

The p-th cohomotopy set of a pointed topological space X is defined by

π ^p(X) = [X,S ^p]

the set of pointed homotopy classes of continuous mappings from X to the p-sphere S ^p. For p=1 this set has an abelian group structure, and is isomorphic to the first cohomology group H¹(X), since S¹ is a K(Z,1). The set also has a group structure if X is a suspension 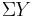, such as a sphere S^q for q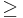1.

Properties

Some basic facts about cohomotopy sets, some more obvious than others:

• π ^p(S ^q) = π _q(S ^p) for all p,q.

• For q = p + 1 or p + 2 ≥ 4, π ^p(S ^q) = Z₂. (To prove this result, Pontrjagin developed the concept of framed cobordisms.)

• If f,g: X → S ^p has ||f(x) - g(x)|| < 2 for all x, [f] = [g], and the homotopy is smooth if f and g are.

• For X a compact smooth manifold, π ^p(X) is isomorphic to the set of homotopy classes of smooth maps X → S ^p; in this case, every continuous map can be uniformly approximated by a smooth map and any homotopic smooth maps will be smoothly homotopic.

• If X is an m-manifold, π ^p(X) = 0 for p > m.

• If X is an m-manifold with boundary, π ^p(X,∂X) is canonically in bijection with the set of cobordism classes of codimension-p framed submanifolds of the interior X-∂X.

• The stable cohomotopy group of X is the colimit

which is an abelian group.